11269. Lemurian parties – easy
King Julien, the ruler of all lemurs, has
exactly 2 ⋅ k lemurs under his command – two lemurs of each of
the k species. Julien loves parties, so every evening he
throws one. However, the VIP area unfortunately has room only for himself
and n other lemurs.
Since Julien dislikes repeating himself, he
wants to invite a set of lemurs to the VIP area that has never appeared before.
Two lemurs of the same species are considered indistinguishable. Two sets of
lemurs are considered the same if they coincide as multisets of species.
Help Julien determine how many distinct
parties he can host. As the answer may be very large, print it modulo 109
+ 7.
Input. A single line contains two integers k and n (1 ≤ k ≤ 500
000, 0 ≤ n ≤ 2 * k) – the number of lemur species and the number of
available VIP seats (excluding Julien himself).
Output. Print one single integer – the number of distinct
parties modulo 109 + 7.
|
Sample
input 1 |
Sample
output 1 |
|
3 3 |
7 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
4 3 |
16 |
SOLUTION
combinatorics
Algorithm analysis
For n seats, some
species will be represented by two lemurs, and some by one. Let i pairs
of lemurs be chosen (that is, i species are represented by two
individuals). The number of ways to make such a choice is 
. After this, there will be n – 2i free seats in the VIP
area. These seats can be occupied by lemurs from k – i remaining
species, choosing one lemur from each. The number of ways to choose such lemurs
is calculated by the formula 
.
Since the value of i
can take any integer from 0 to k, the final answer is obtained as the
sum over all possible values of i:
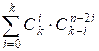
Example
Let’s consider a second
example, where there are k = 4 pairs of lemurs and n = 3 seats in
the VIP area. Using the formula, we get:
= 
+ 
= 4 + 12 = 16
Let’s list
only the nonzero terms. We’ll consider the value 
to be zero if any of the following three
inequalities hold: k < 0, n < 0 or k > n.
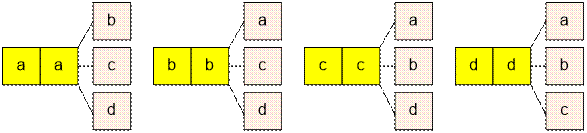
Let us denote the lemurs
by the letters {a, a, b, b, c, c, d,
d}, where
identical letters correspond to lemurs of the same species.
The term = 4 corresponds to the situation where no pair
of lemurs of the same species is chosen, that is, each of the three selected
lemurs belongs to a different species. The four possible selections are as
follows:
Now consider the term = 12. In this case, two lemurs are chosen from
one species (there are 4 possible ways to do this). For the remaining one seat,
one lemur is chosen from the three remaining species. Thus, there are a total
of 12 possible selections.
It is clear that it is
impossible to place two lemurs from two different species in only three seats.
Therefore, all the remaining terms of the sum are equal to zero.
Algorithm implementation
Declare the constants.
#define MAX 1000001
#define MOD 1000000007
Let us define the
following arrays:
·
fact contains the factorials of numbers
modulo MOD;
·
factinv contains the values inverse to the
factorials of numbers modulo MOD:
fact[n] = n!
mod 1000000007
factinv[n] = n!
-1 mod 1000000007
typedef long long ll;
ll fact[MAX], factinv[MAX];
The function pow computes the power of a number modulo p: xn mod p.
ll pow(ll x, ll n, ll p)
{
if (n == 0) return 1;
if (n % 2 == 0) return pow((x * x) % p, n / 2, p);
return (x * pow(x, n - 1, p)) % p;
}
The
function inverse finds the number that is the modular
inverse of x with respect to a prime modulo p. Since p is
a prime number, by Fermat’s little theorem the following equality holds:
xp-1 mod p = 1 for every 1 ≤ x < p
This equality can be rewritten as:
(x * xp-2) mod p =
1,
which means that the modular inverse of x is xp-2 mod p.
ll inverse(ll x, ll p)
{
return pow(x, p - 2, p);
}
The function Cnk computes the value of the binomial
coefficient using the following formula:
=
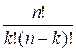
ll Cnk(int n, int k)
{
return ((fact[n] * factinv[k]) % MOD * factinv[n - k]) % MOD;
}
The main part of the program. Read the input data.
scanf("%d %d", &k, &n);
Fill the factorial arrays fact and factinv.
fact[0] =
1;
for (i = 1; i < MAX; i++)
fact[i] = (fact[i - 1] * i) % MOD;
factinv[0]
= 1;
for (i = 1; i < MAX; i++)
factinv[i] = inverse(fact[i], MOD);
Compute the answer using the formula 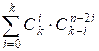. The value of the binomial coefficient is considered to be zero
if any of the following three conditions hold: k < 0, n < 0 or k > n.
res = 0;
for (i = 0; i <= k; i++)
{
if (n - 2 * i < 0 || k -
i < 0 || n - 2 * i > k - i) continue;
res = (res + Cnk(k, i) * Cnk(k - i, n - 2 *
i)) % MOD;
}
Print the answer.
printf("%lld\n", res);